今天笔试有一道题目要求实现最小二乘法，但是我因为没有留意到题目只涉及三个系数、两个因变量，最后在想起被数值分析所支配的恐惧中这道题交了白卷 ╮(╯▽╰)╭ 。

Linear regression

线性回归借助若干个统计样本

$$\begin{array}{} \mathbf{X}=\begin{pmatrix} 1 & x_{11} & \ldots & x_{1n}\\ 1 & x_{21} & \ldots & x_{2n}\\ \vdots & \vdots & \ddots & \vdots\\ 1 & x_{m1} & \ldots & x_{mn}\\ \end{pmatrix} & \mathbf{Y}=\begin{pmatrix} y_1\\ y_2\\ \vdots\\ y_m\\ \end{pmatrix} \end{array}$$

来确定多元线性函数

$y=a_0+a_1x_1+a_2x_2+\ldots+a_nx_n$ 中的系数$\mathbf{A}=(a_0, a_1,a_2,\ldots,a_n)^T$。

Least Square Solution

线性方程组是长这个样子的

$$\mathbf{XA=Y}$$

大多数情况下线性回归问题样本个数 $m$ 不必等于系数个数 $n$，由此衍生出一种针对线性方程组、叫做“最小二乘解”的东西。在这个语境下，方程组的个数小于/大于未知数的个数，不能使用准确的求解方法比如高斯消元法，因此最小二乘解可以看作方程组的近似解。

Method

作为一种解决线性回归问题的方法，最小二乘法作以偏差的平方和最小为目标，即

$$\min{\sum_{j=1}^{m}{(y_j-\sum_{i=0}^{n}{a_ix_{ji}})^2}}$$

可以把上边的多项式视为自变量为$(a_0, a_1,a_2,\ldots,a_n)$的多元函数$f$，于是目标变为

$$f(a_0, a_1,a_2,\ldots,a_n)=\sum_{j=1}^{m}{(y_j-\sum_{i=0}^{n}{a_ix_{ji}})^2}$$ $$\dfrac{\partial f}{\partial a_i}=0$$

The Minimum of $f$

如果要问为什么要使偏导数等于$0$，就要考察一下多元函数$f$的单调性。以对$a_0$求偏导数为例，

$$\dfrac{\partial f}{\partial a_0}=-2\sum_{j=1}^{m}x_{j0}{(y_j-\sum_{i=0}^{n}{a_ix_{ji}})}=2\sum_{j=1}^{m}x_{j0}^2\cdot a_0-2\sum_{j=1}^{m}x_{j0}{(y_j-\sum_{i=1}^{n}{a_ix_{ji}})}$$

这个偏导数在任意一点附近沿 $a_0$ 方向可以理解为一个斜率大于0的线性函数

$$\dfrac{\partial f}{\partial a_0}=ka_0+b \text{ and }k=2\displaystyle\sum_{j=1}^{m}x_{j0}^2=2m> 0$$

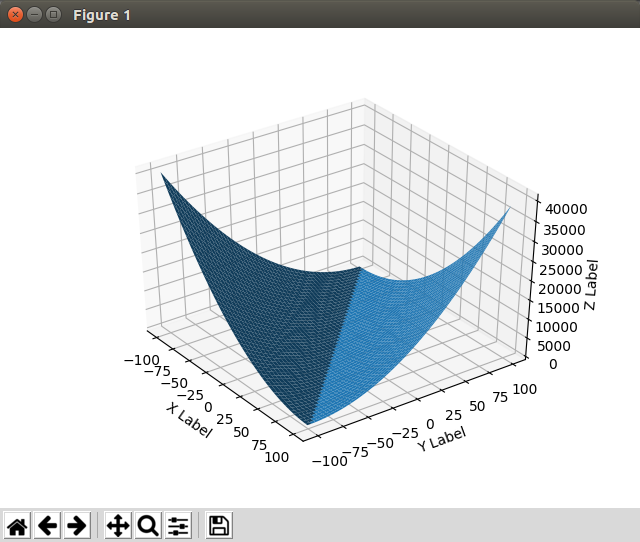
这表示原函数 $f$ 在某些点（比如$\dfrac{\partial f}{\partial a_0}=0$处）的 $a_0$ 方向上先单调下降后单调上升，有极小值；从直观上看，满足所有偏导数值都为$0$的点$(a_0’,a_1’,\ldots,a_n’)$就是令$f$得到最小值的点。可以结合一个二元二次函数的图像看下

Derivation

因此，确定系数$\mathbf{A}=(a_0, a_1,a_2,\ldots,a_n)^T$转化为解线性方程组

$$\begin{cases} \dfrac{\partial f}{\partial a_0}=0 \\ \dfrac{\partial f}{\partial a_1}=0 \\ \ldots\\ \dfrac{\partial f}{\partial a_n}=0 \\ \end{cases}$$

接下来为了方便我自己理解最小二乘法，将对$\dfrac{\partial f}{\partial a_i}=0$ 进行逐步变换。对$a_i$求偏导数将会出来一个系数$x_{ji}$，同时将$y_j$放到等号的另一边

$$\begin{aligned} & \dfrac{\partial f}{\partial a_i}=0 \implies \sum_{j=1}^{m}x_{ji}{(y_j-\sum_{i=i}^{n}{a_ix_{ji}})} =0 \\ \implies &\sum_{j=1}^{m}x_{ji}(a_0x_{j0}+a_1x_{j1}+\ldots+a_nx_{jn})=\sum_{j=1}^{m}x_{ji}y_j\\ \end{aligned}$$

这个时候合并同类项到未知数，即按照$a_0, a_1,\ldots,a_n$归类，

$$\implies a_0\sum_{j=1}^{m}x_{ji}x_{j0} + a_1\sum_{j=1}^{m}x_{ji}x_{j1}+\ldots+a_n\sum_{j=1}^{m}x_{ji}x_{jn}=\sum_{j=1}^{m}x_{ji}y_j$$

结合样本矩阵 $\mathbf{X}$，第一个下标表示行，第二个下标表示列，因此可以观察到在上边方程的左侧，每一个 $a_k$ 的系数都有一个求和，其实是矩阵 $\mathbf{X}$ 的第 $i$ 列与 $\mathbf{X}$ 第 $k$ 列的积；为了体现出矩阵乘法(行x列而不是列x列)，更准确地说，是矩阵$\mathbf{X}^T$的第 $i$ 行与 $\mathbf{X}$ 第 $k$ 列的积。现在可以引出这种以矩阵形式表达的而且易于记忆的形式

$$\begin{pmatrix} \\ \\ x_{0i} & x_{1i} & \ldots & x_{mi}\\ \\ \\ \end{pmatrix} \begin{pmatrix} &&&x_{0k}&&&\\ &&&x_{1k}&&&\\ &&&\vdots&&&\\ &&&x_{mk}&&&\\ \end{pmatrix} \begin{pmatrix} \\ \\ a_k\\ \\ \\ \end{pmatrix}= \begin{pmatrix} \\ \\ x_{0i} & x_{1i} & \ldots & x_{mi}\\ \\ \\ \end{pmatrix} \begin{pmatrix} y_1\\ y_2\\ \vdots\\ y_m\\ \end{pmatrix}$$ $$\mathbf{X}^T\mathbf{XA}=\mathbf{X}^T\mathbf{Y}$$

由 $n$ 个偏导数等于$0$的等式将引出 $n$ 个线性方程，可以使用高斯消元法解出$(a_0,a_1,\ldots,a_n)$。特别地，这个线性方程组的系数矩阵$\mathbf{X}^T\mathbf{X}$是一个对称矩阵($({\mathbf{X}^T\mathbf{X}})^T=\mathbf{X}^T\mathbf{X}$)，因此适用平方根法（比高斯消元法快一半）或者$LDL^T$法(避免开平方)解决。

如果线性函数只有3个或者少于3个系数$a$，就可以直接用克莱姆法则解决。其实笔试题考的应该是这个(/Д`)~ﾟ｡

---

• Next
  A Friendly Introduction to Number Theory Chapter 7

---