Content

Divisibility

Suppose $m$ and $n$ are integers with $m\not=0$. We say that $m$ divides $n$ if $n$ is a multiple of $m$, that is, if there is an integer $k$ such that $n=mk$

Euclidean algorithm

已知$ a\ge b\ge1$，为求 $\gcd{(a,b)}$，令$r_{-1}=a\text{, }r_0=b$，$r_{i-1}=r_{i}q_{i+1}+r_{i+1}\text{, }r_{i}\gt r_{i+1}\text{, } q_{i}\ge1$，

$\begin{aligned} r_{-1} &= r_0q_1+r_1\\ r_0 &= r_1q_2+r_2\\ &\ldots\\ r_{n-3}&=r_{n-2}q_{n-1} + r_{n-1}\\ r_{n-2}&=r_{n-1}q_{n}\\ \end{aligned} \implies r_n=\gcd{(r_0, r_1)}$

欧几里德算法的证明不难。从最后一条的等式， $r_{n-1}\mid r_{n-2}\implies r_{n-1} \mid{(r_{n-2}q_{n-1}+r_{n-1})} \implies r_{n-1}\mid r_{n-3}$

我们自底向上地重复这个步骤，总可以得到 $r_{n-1}\mid r_{-1}\text{, }r_{n-1}\mid r_0$，因此$r_{n-1}\le\gcd{(r_0, r_{-1})}$。

设 $d=\gcd{(r_0, r_{-1})}$。这次我们从第一个等式开始， $d\mid r_0\text{, }d\mid r_{-1}\implies d\mid{(r_{-1}- r_0q_1)} \implies d\mid r_1$

自顶向下地重复这个步骤，最后可以得到 $d\mid r_{n-1}\implies d\le r_{n-1}$，即 $r_{n-1}\ge\gcd{(r_0, r_1)}$。结合 $r_{n-1}\le\gcd{(r_0, r_{-1})}$，所以 $r_{n-1}=\gcd{(r_0, r_{-1})}$

Time complexity

证明在欧几里德算法中，$r{i+2} \le \dfrac{1}{2}r_i\text{ for every }i=0,1,2,\ldots$._

显然，

$r_{i+2} < r_{i+1}\text{ and }q_{i+1}\ge1\implies r_{i+2}\le r_{i+1}q_{i+1}\implies r_{i+2}\le r_i-r_{i+2}\implies r_{i+2} \le \dfrac{1}{2}r_i$

证明欧几里德算法在至多$2\log_2{b}$个步骤后停止。特别地，算法步骤的数量不超过 $b$ 的数位的 $7$ 倍。

被除数和除数经过两次除法后至少减少为原来的$\frac{1}{2}$，可以理解为输入规模减半。然而理解是一回事，证明又是另一回事。Wikipedia 给出一种证明，这个证明方法有意思的地方在于它结合了斐波纳契数列，借助斐波那契数列项的性质反向推出需要执行除法的次数，而且这个证明的上界要小于原问题。

这个证明用到两个推论。首先，用 $F_N$ 表示斐波那契数列的项：

1. 令 $\phi=\dfrac{1+\sqrt{5}}{2}\text{, }\phi^N=F_N\phi+F_{N-1}$ (wikipedia)
2. 假如对 $(a,b)$ 用欧几里德算法求最大公因子需要做 $N$ 次除法，那么 $a\ge F_{N+2}\text{ and }b\ge F_{N+1}$ 。

用归纳法(Induction)证明推论 1：

基础：当$N=1$时，$F_1\cdot\phi+F_0=\phi$，推论成立。

归纳假设：假设推论对$N=k$时成立，即$\phi^k=F_k\phi+F_{k-1}$ 。

递推：当$N=k+1$，应用归纳假设可以得到

$\begin{aligned} \phi^{k+1}&=\phi\cdot(F_k(\phi-1)+(F_{k-1}+F_k))\\ &=F_{k+1}\phi + F_k(\phi-1)\phi\\ &=F_{k+1}\phi + F_k\\ \end{aligned}$

同样地，用归纳法证明推论 2：

基础：当$N=1$时，$a\ge F_3=2\text{ and }b\ge F_2=1$，推论成立。

归纳假设：假设推论对$N=k$时成立，即对 $(a,b)$ 用欧几里德算法求最大公因子需要做 $k$ 次除法，那么$a\ge F_{k+2}\text{ and }b\ge F_{k+1}$ 。

递推：已知对 $(a,b)$ 用欧几里德算法求最大公因子需要做 $k+1$ 次除法。因为 $a=bq_1+r_1$是第一次除法，所以由归纳假设可知对$(b, r_1)$需要 $k$ 次除法，而且 $b \ge F_{(k+1)+1}\text{, }r_1\ge F_{k+1}$。因此$a=bq_1+r_1\ge b + r_1 \ge F_{k+2} + F_{k+1}=F_{(k+1)+2}$。因此推论对 $N=k+1$ 也成立。

由于$F_{N+2}=F_{N+1}+F_N=2F_N+F_{N-1} > \phi^N$，所以$F_{N+1}>\phi^{N-1}$。因此 $b \ge F_{N+1} > \phi^{N-1} \implies N<\log_{\phi}{b}+1$。

特别地，当$N\ge4$，$N<\log_{\phi}{b}+1<2\log_2b$ 。此外，由于$\log_{10}\phi>\dfrac{1}{5}$，

$N-1<\log_{\phi}b=\dfrac{\log_{10}b}{\log_{10}\phi} <5\log_{10}b$

Code snippets

def _gcd(a, b):
    a = abs(a)
    b = abs(b)
    if a == 0 or b == 0:
        return max(a, b)
    while True:
        quot = a // b
        reman = a - b * quot
        if reman == 0:
            return b
        a, b = b, reman

Extended Euclidean algorithm

接着上面的内容。扩展欧几里德算法的目的是计算整数 $s, t$ 满足

$sa+tb=r$

但是我们先要证明这样的整数存在；这个证明的过程同时也是算法实现的过程。接下来，我们需要证明：

每一个余数 $r_i$ 都可以写成 $a$ 和 $b$ 的倍数的和，即

$r_i =s_ia+t_ib$

而且

$\begin{aligned} s_{i+1}&=s_{i-1}-s_iq_{i+1}\\ t_{i+1}&=t_{i-1}-t_iq_{i+1}\\ \end{aligned}$

我们可以大概了解一下思路。注意欧几里德算法中的一个除法步骤

$r_{i-1}=r_iq_{i+1}+r_{i+1} \iff r_{i+1}=r_{i-1}-r_iq_{i+1}$

这表示，假如 $r_i$（以及 $r_{i-1}$ ）能以 $s_ia+t_ib$ （以及 $s_{i-1}a+t_{i-1}b$ ）表示，那么 $r_{i+1}$ 作为 $r_i$ 以及 $r_{i-1}$ 对应项相减 得到的线性组合，理所当然地能够用 $s_{i+1}a+t_{i+1}b$ 来描述；至于起始项，由第一个除法步骤 $a=bq_1+r_1\iff r_1=a-bq_1$，再结合递推式，不难看出 $s_{-1}=1\text{, }s_0=0\text{, }t_{-1}=0, t_0=1$。到这里，归纳法的要素已经齐全了。

基础：当$i=1$，

$r_1=a-bq_1=(s_{-1}-s_0q_1)a+(t_{-1}-t_0q_1)b=s_1a+t_1b$

归纳假设 ：假设当$i=k$时命题成立，即

$r_k=s_ka+t_kb$

递推：那么当$i=k+1$，应用归纳假设

$\begin{aligned} r_{k+1}&=r_{k-1}-r_kq_{k+1}\\ &=(s_{k-1}a+t_{k-1}b) - (s_ka+t_kb)q_{k+1}\\ &=(s_{k-1} - s_kq_{k+1})a + (t_{k-1} - t_kq_{k+1})b\\ &=s_{k+1}a+t_{k+1}b\\ \end{aligned}$

所以命题对 $i=k+1$ 时也成立。而且 $r_n=\gcd{(a,b)}$，因此 $ax+by=r=\gcd{(a,b)}$ 得到证明。

我们还可以用证明形如 $aX+bY$ 的最小正整数只能是 $\gcd{(a,b)}$。从上面的结果可知存在整数 $x,y$ 使得以下等式成立

$ax+by=g=\gcd{(a,b)}$

假设形如 $aX+bY$ 的最小整数为 $c’$，即

$\begin{array}{} ax'+by'=c' &\text{ and } & g=kc+d \end{array}$

首先，我们可以断言 $d=0$，即 $c$ 整除 $g$；否则 $d\gt 0$，

$\begin{aligned} a(x-x')+b(y-y')&=g-c\\ a(x-2x')+b(y-2y')&=g-2c\\ &\ldots\\ a(x-kx')+b(y-ky')&=g-kc=d \end{aligned}$

这表示 $d$ 也能满足条件；但由于 $d\lt c$，这与 $c$ 是满足条件的最小整数矛盾，因此 $d=0$ 而且 $c$ 整除 $g$。但由于 $g\mid a$ 而且 $g\mid b$，因此 $g\mid c$；结合前面 $c$ 整除 $g$，$c=g$，形如 $ax+by$ 的最小整数就是 $\gcd{(a,b)}$。

Code snippets

def _gcd_positive_int(r, g):
    """
    r>=g>0
    """
    sn, sl, sc = 1, 1, 0
    while True:
        quot = r // g
        reman = r - g * quot
        if reman == 0:
            break
        sn = sl - sc * quot
        sl, sc = sc, sn
        r, g = g, reman
    return g, sn

def _gcd_positive_coeff(a, b):
    """
    b % a != 0
    """
    g, s = _gcd_positive_int(abs(a), abs(b))
    s *= abs(a) // a
    if s < 0:
        k = (-s*g)//b
        if b > 0:
            k+=1
        s += k * b // g
    assert s > 0
    return g, s, (g-s*a) // b

def gcd(a, b):
    pa, pb = abs(a),abs(b)
    if 0 in (pa, pb):
        return max(pa, pb)
    elif pa < pb and pb % pa == 0:
        g, s, t = _gcd_positive_coeff(b, a)
        return g, t, s
    else:
        return _gcd_positive_coeff(a, b)
    

Linear equation

形如以下 $ax+by=c$

的方程称为线性方程。这种方程在坐标系上的图像是一条直线，在实数集合上有无数多个解(x,y)，但我们只关心当中的整数解。线性方程 $ax+by=c$ 的解可以借助扩展欧几里德算法描述。

如果 $c \lt \gcd{(a,b)}=g$，线性方程无整数解；接着考虑 $c=g$ 的情况。设线性方程$ax+by=g$的两个解分别为$(x_1,y_1)$ 和 $(x_2,y_2)$，即

$\begin{aligned} ax_1+by_1=g\text{ (1)}\\ ax_2+by_2=g\text{ (2)}\\ \end{aligned}$ $\begin{aligned} \text{(1)}\times x_2-\text{(2)}\times x_1&\implies x_2=\dfrac{b}{g}(x_2y_1-x_1y_2)+x_1\\ \text{(1)}\times y_2-\text{(2)}\times y_1&\implies y_2=-\dfrac{a}{g}(x_2y_1-x_1y_2)+y_1\\ \end{aligned}$

令$k=x_2y_1-x_1y_2$，那么

$\begin{aligned} x_2=x_1+k\dfrac{b}{g}\\ y_2=y_1-k\dfrac{a}{g}\\ \end{aligned}$

只要有了第一个解$(x_1,y_1)$就能得到第二个解(如果有的话)，可以看作$a(x+k\dfrac{b}{g})+b(x-k\dfrac{a}{g})=g$，从 $x$ 减去 $k\dfrac{b}{g}$，将$k\dfrac{a}{g}$ 加到 $y$。

更一般的情况

$ax+by=c$

也是一样的

$\begin{aligned} x_2=x_1+k\dfrac{b}{g}\\ y_2=y_1-k\dfrac{a}{g}\\ \end{aligned}$

Code snippets

from functools import reduce
def linear_equation(*coeff, **kwargs):
    w, s = [], [1]
    g = coeff[0]
    for b in coeff[1:]:
        g, wi, si = gcd(g, b)
        s.append(si)
        w.append(wi)
    w.append(1)
    c = kwargs.pop('c', g)
    if c % g == 0:            
        r = []
        reduce(lambda p, t: r.insert(0, p * t[1] * t[0]) or p * t[1], zip(reversed(s), reversed(w)), c // g)
        return r

Two relatively prime integers

最后补充一个 $a$ 和 $b$ 互质的 充分必要条件

$\exists x,y\in\mathbb{Z}\text{ s.t. }ax+by=1\iff\gcd{(a,b)}=1$

Exercises

5.4

(b) && (c)

找出并证明最小公倍数 $\text{LCM}(m,n)$ 和 $m\text{, }n\text{ and }\gcd{(m,n)}$ 的关系

列举几个例子之后可以发现关系 $\dfrac{mn}{\gcd{(m,n)}}=\text{LCM}(m,n)$

令 $m=a\gcd{(m,n)}\text{, }n=b\gcd{(m,n)}\text{ and }\gcd{(a,b)=1}$，

$\dfrac{mn}{\gcd{(m,n)}}=a\cdot b\cdot\gcd{(m,n)}=b\cdot m=a\cdot n \implies \text{LCM}(m,n)\mid\dfrac{mn}{\gcd{(m,n)}}$

因为 $\gcd{(a,b)=1}$，所以$\dfrac{mn}{\gcd{(m,n)}}$是最小的公倍数，即$\dfrac{mn}{\gcd{(m,n)}}=\text{LCM}(m,n)$。

(d)

已知 $\gcd{(m,n)}=18\text{, LCM}(m,n)=720$。满足条件的 $m\text{ and }n$是否不止一对?

$\begin{aligned} m &= 18a\\ n &=18b\\ \end{aligned}\bigg\}\implies18ab=720\implies ab=40\text{ }(\gcd{(a,b)}=1)$

满足条件的有

$(a,b)=(1,40)\text{ or }(5,8)\implies(m,n)=(18,720)\text{ or }(90,144)$

像这样给出最大公因子和最小公倍数然后要找出$(m,n)$的问题，因为整数总有一个因子为$1$，所以至少有一对满足条件的数字；假如 $\dfrac{\text{LCM}(m,n)}{\gcd{(m,n)}}$是一个合数，那么这样的数对不止一个。算术基本定理表示任意一个整数都可以写作$A=1\cdot q_1^{k_1}q_2^{k_2}\ldots q_N^{k_N}\text{, }\gcd{(q_i,q_j)}=1$。将拥有$M$个元素的集合划分为两堆，一共有 $2^{M-1}-1$ 种不同的划分方式（即集合的非空真子集个数）。因此满足给定条件的数对一共有$1+(2^{(N-1)-1}-1)=2^{N-2}$对。

另外关于将集合划分成两堆的问题也可以看作从$A$中取1/2/3/…个元素。

5.5

Collatz Conjecture

Consider the following operation on an arbitrary positive integer:

If the number is even, divide it by two.

If the number is odd, triple it and add one.

… Now form a sequence by performing this operation repeatedly, beginning with any positive integer, and taking the result at each step as the input at the next.

(c)

假设算法都能在值为 $1$ 的时候终止，令$L(n)$表示算法在起始值为 $n$ 的长度。比如 $L(5)=6\text{ and }L(7)=17$ 。证明假如 $n=8k+4$那么 $L(n)=L(n+1)$。

$\begin{aligned} n=8k+4=2^2(2k+1) &\xrightarrow{3(2k+1)+1} 2(3k+2)\rightarrow 3k+2\\ n+1=8k+5 &\xrightarrow{3(8k+5)} 2^3(3k+2)\rightarrow 3k+2\\ \end{aligned}$ $\implies L(n)=L(n+1)=4+L(3k+2)$

(d)

证明假如 $n=128k+28$，那么$L(n)=L(n+1)=L(n+2)$。

与(c)类似，最后$L(n)=L(n+1)=L(n+2)=81k+20$

(e)

找出更多与(c),(d)相似的条件。

5.6

实现 5.5 算法并收集收据

def f(n):
    ls = n
    seen = {n}
    while True:
        if ls % 2 == 0:
            nx = ls //2
        else:
            nx = 3*ls+1
        if nx in seen:
            break
        else:
            seen.add(nx)    
            ls = nx
    return ls, seen

count = 1000

terminates = {}
for i in range(count):
    t, s = f(i)
    terminates[i] = (t, len(s))


results = np.array(list(terminates.values()))
plt.scatter(np.arange(count), results.transpose()[-1])
plt.show()

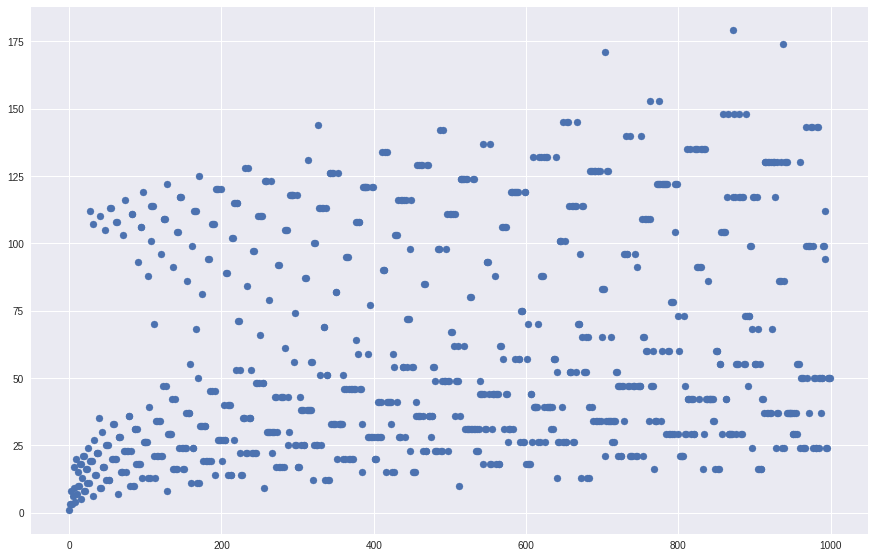
Length of the algorithm for $N<10000$

plt.scatter(np.arange(count), results.transpose()[0])
plt.show()

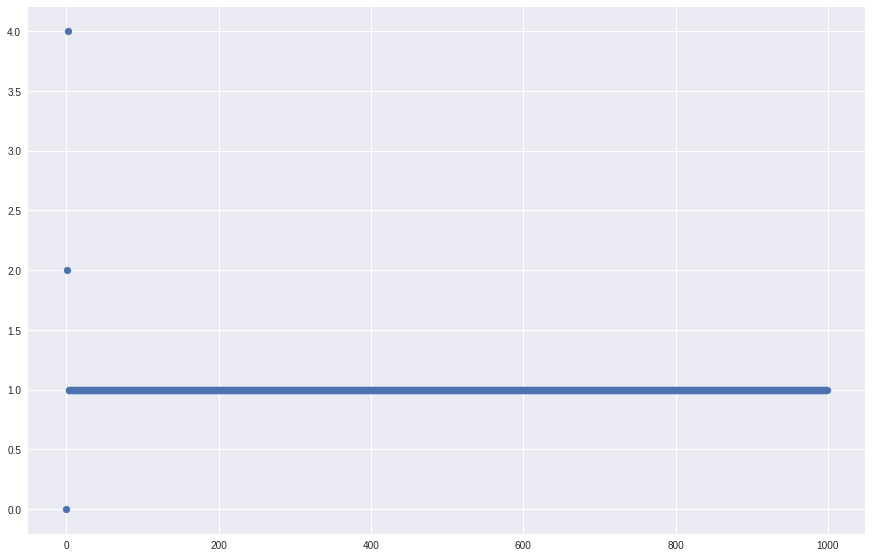
Terminating values for $N<10000$

在 $N<10000$ 内，除了$N=1\text{ and }N=2$以外，其他值的Terminating value都是 $1$ 。

import collections

stat = collections.defaultdict(list)
for i, r in enumerate(results):
    _, l = r
    stat[l].append(i)

6.6

关于线性方程 $ax+by=c$ 的非负解 $(x\ge0\text{, }y\ge0)$：

(a)

解释为何 $3x+5y=4$ 无正整数解。

$x$	$y$	$3x+5y$
0	0	0
0	1	5
1	1	8
1	0	3

而且当$x\ge1\text{, }y\ge1\text{, }3x+5y\ge8$，所以 $3x+5y=4$无整数解。

(b)

列出一些例子说明 $3x+5y(x\ge0\text{, }y\ge0)$ 不可能为哪些值？

def diff(side, func):
    res = set()
    for i in range(side):
        for j in range(side):
            res.add(func(i,j))
    return sorted(set(range(func(side-1,side-1)+1))-res)

>>> diff(10, lambda x,y:3*x+5*y)
[1, 2, 4, 7, 65, 68, 70, 71]
>>> diff(20, lambda x,y:3*x+5*y)
[1, 2, 4, 7, 145, 148, 150, 151]
>>> diff(100, lambda x,y:3*x+5*y)
[1, 2, 4, 7, 785, 788, 790, 791]

可以从脚本输出结果猜测$3x+5y(x\ge0\text{, }y\ge0)$的取值为$\mathbb{Z}^\ge-{1,2,4,7}$

(c)

对于$(a,b)$为下列取值的时候，$ax+by$不可能为哪些取值？

$\begin{array}{} \text{(i) } (a,b)=(3,7) & \text{(ii) } (a,b)=(5,7) & \text{(iii) } (a,b)=(4,11)\\ \end{array}$

>>> diff(100, lambda x,y:3*x+7*y)
[1, 2, 4, 5, 8, 11, 979, 982, 985, 986, 988, 989]
>>> diff(100, lambda x,y:5*x+7*y)
[1, 2, 3, 4, 6, 8, 9, 11, 13, 16, 18, 23, 1165, 1170, 1172, 1175, 1177, 1179, 1180, 1182, 1184, 1185, 1186, 1187]
>>> diff(100, lambda x,y:4*x+7*y)
[1, 2, 3, 5, 6, 9, 10, 13, 17, 1072, 1076, 1079, 1080, 1083, 1084, 1086, 1087, 1088]
>>> diff(100, lambda x,y:2*x+7*y)
[1, 3, 5, 886, 888, 890]

(d) && (e)

试描述不能够用$ax+by(x\ge0\text{, }y\ge0\text{, }\gcd{(a,b)}=1)$表示的最大整数并证明。

从上边的四个例子很容易猜测这个整数为 $ab-(a+b)$。先考虑线性方程 $ax+by=ab\text{, }\gcd{(a,b)}=1$

的正整数解。因为$ax=ab-by=b(a-y)$而且$\gcd{(a,b)}=1$，所以$b\mid x$。同理可以得到$a\mid y$。所以令$x=kb\text{, }y=ha\text{, }k\ge0\text{, }h\ge0$，

$\begin{aligned} ax+by&=ab\\ a\cdot kb+b\cdot ha&=ab\\ k+h&=1\\ \end{aligned} \implies \begin{cases} k = 0 \text{ or }1\\ h = 1 \text{ or }0\\ \end{cases} \implies \begin{cases} x = 0 \text{ or }b\\ y = a \text{ or }0\\ \end{cases}$

因此线性方程$ax+by=ab$的解为$(0,a)\text{ or }(b,0)$。由于

$\begin{aligned} &x+1=0\implies x=-1\\ &y+1=0\implies y=-1\\ \end{aligned}$

跟 $x\ge0\text{, }y\ge0$ 矛盾，所以线性方程$a(x+1)+b(y+1)=ab$无正整数解，即不存在$(x,y)\text{, }x\ge0\text{, }y\ge0$ 使得$ax+by=ab-(a+b)$。

后来发现 wikipedia 上边有这个问题，名字叫做“硬币问题”。

(f)

如果换作是三个系数的和 $ax+by+cz$ ，情况又是怎样的呢？

To be continued.

A Friendly Introduction to Number Theory Chapter 5~6

欧几里德算法(Euclidean algorithm)

Content

Divisibility

Euclidean algorithm

Time complexity

Code snippets

Extended Euclidean algorithm

Code snippets

Linear equation

Code snippets

Two relatively prime integers

Exercises

5.4

(b) && (c)

(d)

5.5

(c)

(d)

(e)

5.6

6.6

(a)

(b)

(c)

(d) && (e)

(f)

FEATURED TAGS

FRIENDS